Enoncé du problème

La firme MAGIX monte sous licence deux types d’ordinateurs compatibles IBM : le PT133 et le DX4100. Les ordinateurs sont montés dans la section Montage puis sévèrement testés dans la section Test. Il faut 4 heures pour monter le PT133 et 3 heures pour le DX4100. Le test du PT133 prend 2 heures tandis que celui du DX4100 n’en prend qu’une. La section Montage ne peut travailler plus de 3600 heures par an tandis que la section Test ne peut dépasser 1400 heures d’activité. La firme MAGIX ne peut écouler plus de 500 PT133 ni plus de 1000 DX4100 par an. Elle réalise un bénéfice de 4500 sur le PT133 et de 3000 sur le DX4100.

Travail à faire : Quelles sont les quantités de PT133 et de DX4100 que doit produire la firme MAGIX par an, pour maximiser son profit ? Quelle est la valeur de ce profit ?

Formalisation du problème

Le problème de la firme MAGIX est un problème de recherche de la combinaison des produits (product-mix) à fabriquer avec des ressources limitées à usage alternatif par une entreprise multi-produit pour maximiser son profit total.

Définition des variables
X : la quantité de PT133 à produire avec un profit unitaire de :   a=4500,
Y : la quantité de DX4100 à produire avec un profit unitaire de : b=3000,
Z : le profit total : Z=aX+bY, soit Z= 4500X+3000Y.

Objectif
L’objectif de la firme MAGIX est de déterminer les quantités X et Y qui maximisent son profit total Z.

Contraintes

Contraintes techniques
(1) Contrainte de la section Montage en heures : 4 X + 3 Y <= 3 600
(2) Contrainte de la section Test en heures :       2 X +    Y <= 1 400

Contraintes commerciales
(3) Contrainte de commercialisation du PT133 :   X <=    500
(4) Contrainte de commercialisation du DX4100 : Y <= 1 000

Contraintes de signe ou contraintes logiques
X >= 0 et Y >= 0 car on ne peut pas produire des quantités négatives ici.

Résumé du programme

Le programme à résoudre suit.

Max Z = 4500X + 3000Y

Sous les contraintes :
(1) 4 X + 3 Y <= 3 600
(2) 2 X +    Y <= 1 400
(3)    X          <=    500
(4)             Y <= 1 000
avec les contraintes de signe X >= 0 et Y >= 0.

A propos de la dénomination « programmation linéaire »

Ce modèle est « linéaire » parce que la fonction « objectif » est linéaire ainsi que les contraintes. La représentation dans le plan (xOy) de l’objectif ainsi que de chaque contrainte, donne une ligne droite et non une ligne courbée. Il s’agit d’un problème basique d’Algèbre linéaire comme le suggère la présentation matricielle ci-après. Mais quid du mot «programmation» ? Il a été proposé vers 1947 par par le savant George Dantzig qui a implémenté l’algorithme de simplexe permettant de résoudre ce genre de problème, dans les ordinateurs par … programmation. Vu que le mot programmation est de plus en plus associé à l’informatique, les spécialistes parlent maintenant d’« optimisation linéaire », pour signifier la recherche d’un optimum (maximum ou minimum selon le cas) d’un problème linéaire. La programmation informatique n’est qu’une modalité de résolution de ces problèmes linéaires d’optimisation.

.

Présentation matricielle

Cette section est destinée aux Etudiants d’Elyth®. Elle peut être ignorée sans nuire à la compréhension du reste de l’article, même si la mise en forme du programme dans le tableur, s’inspire largement de cette présentation !

Introduction des vecteurs et matrices

Soient :
P : le vecteur colonne des produits, de type 2 lignes, 1 colonne, soit (2,1).
C : le vecteur des profits unitaires, de type 1 ligne, 2 colonnes, soit (1,2).
Z : la valeur du profit total, un scalaire, 1 ligne, 1 colonne, soit (1,1).

Vérification de la faisabilité du produit matriciel CP->Z : (1,2)(2,1)->(1,1). OK.

A : la matrice des coefficients des quatre contraintes, de type 4 lignes, 2 colonnes, soit (4,2).
B : le vecteur colonne des valeurs limites de type 4 lignes, 1 colonne, soit (4,1).



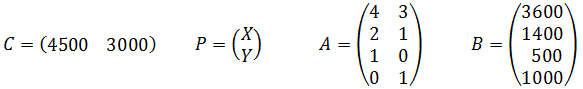
Vérification de la faisabilité du Produit matriciel AP->B : (4,2)(2,1)->(4,1). OK.

Ecriture matricielle du programme

Max Z=CP
sous
AP<=B

ou encore

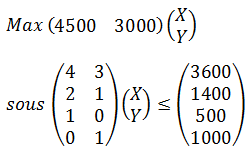
Résolution avec le Solveur de Microsoft® Excel™

Ce programme peut être résolu :
- graphiquement car il n’y a que deux variables,
- par l’algorithme de simplexe avec les tableaux,
- avec des programmes informatiques comme Microsoft® Excel™, choisi pour cet article.

Mise en forme du programme dans le tableur

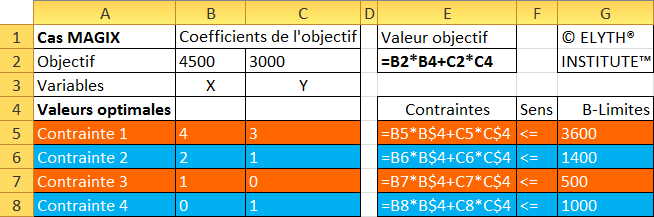
La cellule E2 est destinée à contenir la valeur optimale.
Les cellules B4 et C4 sont destinées à contenir respectivement les variables X et Y.
Les cellules E5,E6,E7,E8 sont destinées aux valeurs des contraintes.

Formulation de l’objectif et du membre gauche de la contrainte

Contenu de la cellule objectif : E2=B2*B4+C2*C4

Calcul des valeurs des contraintes

     Contrainte 1 : E5=B5*B$4+C5*C$4
     Contrainte 2 : E6=B6*B$4+C6*C$4
     Contrainte 3 : E7=B7*B$4+C7*C$4
     Contrainte 4 : E8=B8*B$4+C8*C$4

La ligne 4 est bloquée dans B$4 et C$4 par le symbole $ en vue de la recopie vers le bas.

Ces valeurs calculées doivent être inférieures ou égales aux valeurs exprimant les disponibilités maximales :
     E5<=G5
     E6<=G6
     E7<=G7
     E8<=G8

Résolution du programme avec le Solveur d’Excel

Une fois le problème posé sous forme de tableau, il faut appeler le Solveur par le Menu selon la version d’Excel. Le Solver est une macro complémentaire Solver.xla ou Solver.xlam qui n’est pas installée par défaut. Il faut chercher dans l’aide d’Excel, comment l’installer.



Si l’installation réussit, le Solver est alors disponible dans le menu [Données] ou dans le Menu [Outils], Sous-menu [Options] dans les très anciennes versions.



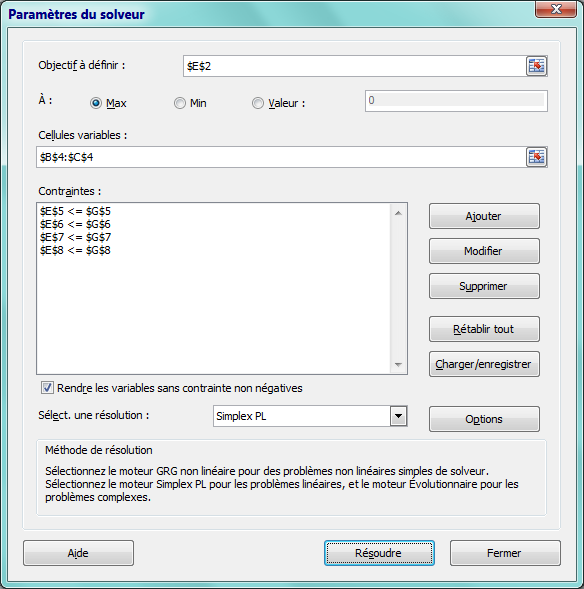
Remarques

1. Les contraintes de signe sont prises en compte en cochant la case « Rendre les variables sans contrainte non négatives ».

2. Comme, le problème à résoudre relève de la programmation linéaire, la méthode de résolution à sélectionner est : Simplex PL (Programmation Linéaire).

3. Ecriture des contraintes dans le Solveur

La colonne F contenant les sens de l’inégalité est figurative pour la lisibilité du tableau. La boîte de dialogue [Ajouter une contrainte] permet de choisir le sens. Il faut ajouter successivement les quatre contraintes. Les cellules E5,E6,E7,E8 sont respectivement comparées avec les valeurs limites contenues dans G5,G6,G7,G8.



Après avoir transposé le problème dans le Solver, il faut activer le bouton de commande [Résoudre] dans la boîte de dialogue [Paramètres du Solveur]. La boite de dialogue [Résultat du solveur] apparaît. Il faut activer les trois Rapports proposés.



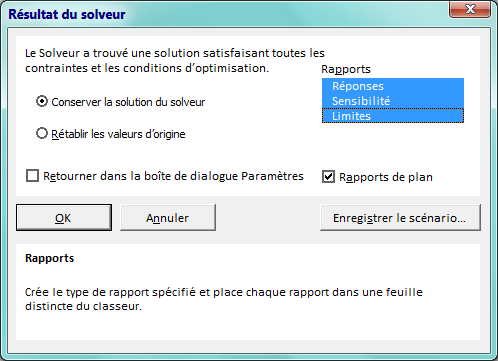
La solution apparaît dans le tableau.



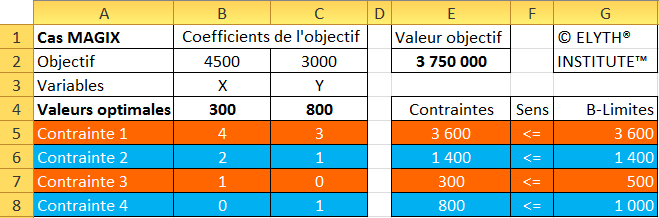
Le nombre de chaque type de machine à produire et la valeur de l’objectif sont affichés dans les cellules prévues à cet effet dans le tableau (X=300, Y=800, Z=3 750 000).

Pour maximiser son profit, la firme MAGIX devra produire 300 unités de l’ordinateur PT133 et 800 unités de l’ordinateur DX4100, ce qui lui procurera un profit total de 3 750 000.

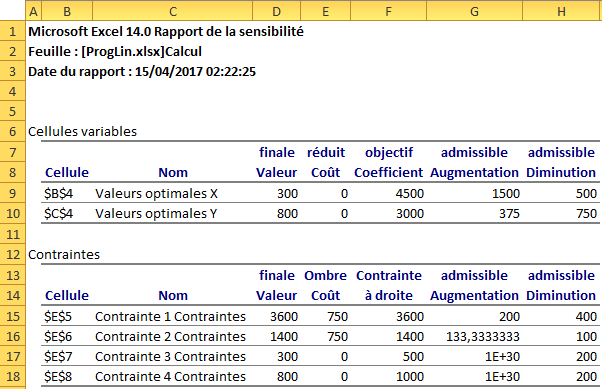
Rapports du Solveur

Le Solveur est un outil puissant qui propose en plus du résultat,un Rapport sur les Réponses, un Rapport de sensibilité et un Rapport des limites.



Saturation, dualité et shadow price

Lorsqu’à l’optimum, la partie gauche de la contrainte est égale à la valeur limite à droite, on dit que la contrainte est « liée » ou « saturée ». C’est le cas des deux premières contraintes. Dans le cas contraire, on dit que la contrainte est « non liée » ou « non saturée ». C’est le cas des deux dernières contraintes. La différence est appelée « marge ».



Le programme résolu ci-dessus peut être considéré comme le premier, le «programme primal ». On peut en déduire le programme réciproque, le « programme dual ». Si l’objectif primal est à maximiser, alors l’objectif dual sera à minimiser, et vice versa. La dualité permet d’établir que le coût marginal (shadow price) d’une ressource non saturée est nul car c’est une ressource « abondante », disponible en excès.

Sources

Cet article initialement intitulé « Résolution de Programme linéaire avec le Solveur » est extrait du cours de Techniques Quantitatives Appliquées à la Gestion (TQAG) de Magloire LANHA à l’Université Nationale du Bénin (1994-2000). L’énoncé et la résolution graphique sont initialement publiés dans Le livre « Manuel d’entraînement en Comptabilité Analytique » de Charles KOUPHIN et Magloire LANHA, Langel Editions, Cotonou, 1991, 100p. ELYTH® ACADEMIC PUBLISHING™ rééditera bientôt ce livre, revu, mis à jour et augmenté. Les titulaires d’un compte gratuit d’ELYTH®, pourront bientôt réserver leur exemplaire dans le menu [Mon Elyth], sous-menu [Mes Livres d’Elyth].

A propos de l’auteur

Magloire LANHA est Professeur Titulaire (Full Professor), Agrégé des Facultés d’Economie et de Gestion.
Il est auteur de nombreux Articles, Manuels, Logiciels et Formations en ligne sur le site d’Elyth® : www.elyth.net.
Vous pouvez lui écrire à l'adresse : maglanha@elyth.net

© ELYTH® INSTITUTE™ - PUBLIE 15 AVRIL 2017 - MIS A JOUR 02 AVRIL 2019