MagSoftNews

 

FRACTALES & CHAOS, Une Introduction

 

LES PRÉCURSEURS

Les fractales existent depuis la nuit des temps, mais elle n'ont connu de  succès  que  récemment  grâce  à  une théorie plus percutante : la théorie du chaos. Il y a longtemps, APOLLONIUS, JULIA  FATOU, CANTOR, KOCK, SIERPINSKI nous ont offert une collection de monstres mathématiques. Mais pour propulser les fractales, il aura fallut que, contre EUCLIDE, Benoît MANDELBROT  nous rappelle la nature fractale de notre univers : les nuages ne sont pas des  sphères,  les montagnes ne sont pas des cônes, les lignes des cotes ne sont pas des cercles, les  écorces  des arbres  ne sont pas lisses,  et l'éclair  non plus, ne se déplace  selon  une  ligne  droite  [The fractal geometry of nature].

 

IMAGES FRACTALES, le simple produit le complexe

 

 

 Le propre des fractales est de contenir une structure souvent simple qui se reproduit infiniment  en  elle-même  à des échelles différentes. Leur succès repose sur le fait qu'elles sont générées par des informations initiales simples qui, par une suite infinie d'itérations, reproduisent  les éléments de la nature : arbres, feuilles, montagnes, rivières  ou encore mieux, des images hautement esthétiques.

 L'ÉQUATION LOGISTIQUE,  Modèle de l'Écologie 

 Pour simuler l'évolution d'une population dans des conditions malthusiennes, les écologistes représentés par Robert MAY ont formulé et étudié la célèbre équation logistique  : P_t+1=r*P_t(1-P_t) , où  :  P_t   est   la Population  actuelle  normée, soit  en  fait  un taux  d'occupation  de  l'environnement.

P_{t+1 :} est la Population normée de l'instant suivant, 1 : la population maximum possible dans les contraintes définies ; (1-P_t) est alors l'espace libre pour naître et vivre, le potentiel biotique ; (1-P_t) induit donc un feed-back  dans le processus ;  r est le paramètre de contrôle ou taux de croissance ou de fécondité etc. L'équilibre à long terme de ce beau petit monde (ou modèle mathématique) dépend de P_{0 :} la population initiale et du paramètre de contrôle r

 

LA ROUTE DE DOUBLEMENT DE PÉRIODE VERS LE CHAOS

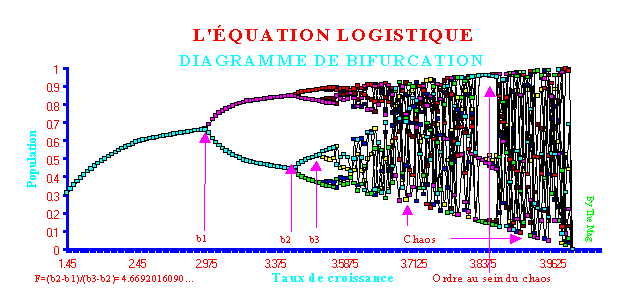
En étudiant les valeurs d'équilibre des systèmes dynamiques comme l'équation logistique, on constate que : - Tant que (r<b1) un léger accroissement de r entraîne une hausse de la valeur d'équilibre de la population. C'est ce qui était généralement admis. - La première bifurcation a lieu à r=b1. Quand (b1<r<b2), la valeur d'équilibre oscille entre deux valeurs pour prendre alternativement l'une et l'autre. Quand (b2<r<b3), quatre valeurs d'équilibre sont alors possibles. René THOM a exprimé les bifurcations en termes de Théorie des catastrophes. - Au-delà de r=b3, le système peut prendre une infinité de valeurs d'"équilibre" exhibant brusquement un  comportement  apparemment  imprévisible, chaotique. Cette cascade de bifurcations est  dénommée "la route vers le chaos".

 

L'ORDRE ÉMERGE DU CHAOS

La théorie du chaos n'est pas comme son nom peut  laisser  croire  une théorie pessimiste ou destructrice. Au contraire, elle montre que dans la zone où le phénomène a un comportement chaotique,   en regardant de près, en mettant la loupe ou le microscope on y retrouve le même motif  [pattern] exhibé par le processus.  La zone  chaotique  est  fractale. Dans  ce  désordre apparaît  un  ordre  absolu, la répétition infinie de la même fractale. Sur le graphique apparaît  grâce à la magnification une fenêtre dans le chaos semblable à celle séparant les deux branches après b1 . Le chaos et les processus dissipatifs loin de l'équilibre seraient  indispensables à la vie (Ilya PRIGOGINE)

 

UN DÉSORDRE A UN RYTHME ORDONNÉ

Un chaos réellement aléatoire serait sans utilité pour la Science et les prévisions. Edward LORENZ, le pionnier, était météorologue. Heureusement, Mitchell FEIGENBAUM a découvert que le désordre se produit à un taux ordonné qui est devenu sa constante F (voir sur le diagramme de bifurcation). Ainsi on peut prévoir le "moment"  exact ou plutôt la valeur critique du paramètre de contrôle où  a  lieu chaque bifurcation,  car les systèmes paraboliques non-linéaires bifurcatifs obéissaient à la constante  de  Feigenbaum F = 4,6692016090...  Comme  quoi,  l'univers recèle bien de chiffres transcendants, les clés de la géométrie, comme  p (rapport constant entre la circonférence et le diamètre de tout cercle) et e (le nombre d'Euler, le même qui est immortalisé sur le billet de 10 Francs Suisses) dont  la  découverte permet aux êtres humains de lui arracher de plus en plus de ses secrets...

 

VERS UNE NOUVELLE SCIENCE ou un nouveau paradigme de la science

Les fractales et la théorie du Chaos,  en élargissant le champs de  la géométrie  vers  davantage  de  réalité  ont  aussi  suscité beaucoup d'espoir (et quelques succès déjà) dans tous les domaines dont la météorologie, l'écologie, la biologie, la cardiologie, la biochimie, la physique, l'astronomie,  l'économie etc.   Partout, les chercheurs tentent de retrouver les processus fractals-chaotiques qui seraient à la base de l'Univers,  de la de Vie,  de la dynamique des Institutions, des cours sur les marchés financiers.

 

L'ENJEU FRACTAL

Si on sait que la connaissance de telles lois pourrait permettre de fonder un nouveau paradigme de La Science  en  même  temps  que faire gagner,  ceteris  paribus,  de  sommes  faramineuses aux premiers ou aux meilleurs,  on comprend pourquoi cette science numérique  alliant  les mathématiques (outil universel de modélisation),  et  l'informatique (outil permettant de simuler in electro en quelques  secondes, ce que Dame Nature mettrait des années ou des millénaires à accomplir), ne  laisse  indifférents  ni  les savants   soucieux   d'aider   le   monde,   ou en  quête  de  gloire (en témoigne la bataille chaotique des fondateurs entre eux pour se faire reconnaître et/ou pour tenter de diminuer la valeur des recherches leurs concurrents), encore moins les jokers de la finance nouvelle. 

By The Mag

---

 

1993 MagSoft     -   Citation avec indication de la source autorisée sans formalité    -     Réf. : MagSoftPub 2930301001