MagSoftNews

MSN n° 005 du 01/07/93 Revue des Softivores Editée par MagSoftPub

:

INTRODUCTION AUX FRACTALES

Les fractales existent depuis la nuit des temps, mais elle n'ont connu de succès que récemment grâce à une théorie plus percutante : la théorie du chaos. Depuis l'Antiquité, APOLLONIUS de PERGA mathématicien et astronome Grec (vers 262-180 avant J.-C.) avait déjà introduit le problème des cercles fractals. Beaucoup plus tard, pendant la 1ère Guerre Mondiale, Gaston JULIA et Pierre FATOU ont étudié les ensembles et courbes de JULIA. Georg CANTOR a inventé sa poussière, Von-KOCK et PEANO leurs Courbes, SIERPINSKI ses triangles ou tapis etc, une véritable collection de "monstres" mathématiques. Mais il aura fallut attendre les années 70 pour que Benoît MANDELBROT, nous rappelle la nature fractale de notre univers dans The fractal geometry of nature, forgeant pour le français, le substantif féminin fractale(s), et l'adjectif fractal(s) ; pour l'anglais, le nom fractal(s) et l'adjectif fractal.

Contrairement aux concepts de la géométrie euclidienne, les fractales sont des objets de dimension non entière ou fractionnaire. Les points, lignes, surface, cônes, cube etc, sont des objets crées par l'esprit humain ... contrairement à Dame Nature qui préfère des formes plutôt fragmentées : lignes brisées de l'éclair, ou chemin tortueux des rivières, surfaces rugueuses de la terre, montagnes non coniques, icebergs non cubiques etc.

Le succès des fractales repose sur le fait qu'elles sont générées par des informations initiales extrêmement simples qui, par une suite infinie d'itérations, reproduisent les éléments de la nature : arbres, feuilles, montagnes, rivières ou encore mieux, des images hautement esthétiques. La géométrie fractale serait donc par essence la "vraie" géométrie de la nature.

La plupart des fractales présentent une homothétie interne leur conférant un aspect scalant (self-similarity) : en les regardant de près ou de loin on retrouve la même forme, chaque partie ressemble au tout. Mais il existe aussi des fractales ne présentant apparemment aucune auto-similarité.

Les fractales "géométriques" sont déterministes et présentent une parfaite symétrie. Mais pour imiter la nature, on introduit un facteur de hasard, générant ainsi des fractales "naturelles" dont la symétrie est moins parfaite : les configurations de la main (paume et doigts ) et du pied (plante et orteils) illustrent ce genre de fractales où les deux objets sans être identiques présentent des similitudes évidentes.

Le processus de génération de la plupart des fractales est un système dynamique non linéaire. Ces dynamiques sont connues comme exhibant des comportements chaotiques. La découverte la plus intéressante est que la zone chaotique d'un diagramme de bifurcation est fractale. Dans ce désordre apparaît un ordre, la répétition infinie de la même fractale. Cet ordre universel, indépendant du processus choisi, est représenté par la constante de Feigenbaum. Le numéro 2 de MagSoftNews introduit la relation Fractales et Chaos.

Cette édition de FRACTALEXPO 1993 consacrée aux Mandelbroïdes, présente aussi des images fractales des processus chaotiques célèbres : attracteur "étrange" de LORENZ et diagramme de bifurcation de Feigenbaum, ainsi que d'autres fractales "naturelles" ...

SECTION 1 : L'ENSEMBLE DE MANDELBROT

Plaque N° 01 : Vue synoptique de l'Ensemble de Mandelbrot

1.1 - L'information génératrice

L'Ensemble de Mandelbrot (noté EM dans cette expo) est produit par l'itération dans le plan complexe de la fonction dynamique z_t+1 = (z_t)² + c , où z₀ = 0 et c le nombre complexe à tester. En coordonnées cartésiennes c = a + ib, où a est l'abscisse mesurée sur l'axe réel, b l'ordonnée sur l'axe imaginaire, i le nombre imaginaire défini par i² = -1.

1.2 - Le processus itératif et le test d'appartenance

A chaque point c du plan complexe (maillage), on fait subir la transformation de Mandelbrot. A chaque itération t on fait le test d'appartenance à l'EM ; deux cas sont possibles :

- la valeur courante de z_t s'échappe de l'origine du plan complexe z₀(0,0) et tend vers l'infini ; on dit aussi qu'elle est explosive. C'est le cas lorsque |z_t|>2 où |z_t| est la norme ou module de z_t : |z_t|=(a² + b²). Le point testé n'appartient pas à l'EM, son attracteur est l'Infini ;

- la valeur courante est stable : |z_t|2 ; on poursuit l'itération et on refait le test. Si au bout d'un nombre T relativement grand d'itérations (par exemple T=100) la valeur finale est stable, le point initial c appartient à l'EM ; son attracteur est le bassin de Mandelbrot. Souvent, les points de l'EM sont marqués en noir ; pour des raisons pratiques d'impression dans cette exposition, les points de l'EM sont marqués en jaune et parfois en blanc (pas d'impression) ; cette couleur de l'EM sera désignée la couleur n° 0 pour la suite de ce texte.

1.3 - Le choix des couleurs et l'esthétique

Pour un catalogue ou palette de 10 couleurs, les points stables jusqu'à la 90ème itération mais qui finalement explosent avant la T=100ème sont très proches de l'EM. On choisit de les marquer de la couleur n° 1, par exemple le magenta. Les points qui explosent entre la 80ème et la 90ème itération sont marqués de la couleur n° 2, par exemple le cyan, ... et les points qui bifurquent vers l'Infini avant la 10ème itération sont marqués de la couleur n° 10, par exemple le bleu.

Avant d'être des choix esthétiques, les couleurs représentent donc de l'information, le "moment" auquel le processus appliqué au point, bifurque vers l'un de ses attracteurs ... Mais les maîtres de l'art ont réussi à faire adopter les fractales par une combinaison de palettes les plus sophistiquées en retournant même l'image sous toutes ses formes et en magnifiant ses confins les plus spectaculaires...

Plaque N° 02 : Vue en miroir de l'Ensemble de Mandelbrot

1.4 - Premiers pas : Un algorithme lisible de l'EM

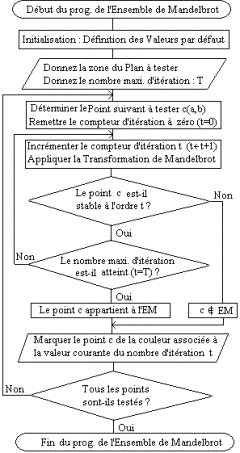
1.5 - L'optimisation des programmes fractales

Couramment, un algorithme est dit optimisé lorsqu'il résout le problème de la manière la plus rapide possible : il s'agit donc de la minimisation du temps d'exécution. Mais l'optimisation rend la lecture d'un programme plus difficile, même pour un programmeur averti. En laissant au programmeur les détails d'optimisation, l'algorithme ci-dessus gagne en lisibilité pour les lecteurs MagSoftNews .

Les programmeurs ont à coeur le problème d'optimisation, au point où, en programmant en langage évolué (C, Pascal, ou encore de cinquième génération) , ils n'hésitent pas à sous-traiter une partie de leur code auprès d'un autre langage plus proche de la machine (en général, l'Assembleur). Pour se rendre compte du caractère crucial de l'optimisation en termes de fractales il suffit de penser aux milliards d'années que Dame Nature a dû mettre depuis le Big Bang pour faire le modeste Honnête Homme de la fin du 20ème siècle, le Softivores.

Les "moteurs" qui consomment le plus de temps sont les boucles, mais aussi les formules mathématiques "élégantes". Par exemple un processeur exécute beaucoup plus rapidement l'instruction x=a+a que x=2*a qui pourtant sont mathématiquement identiques. Comme leurs créateurs humains, les ordinateurs préfèrent les additions aux multiplications. Dans le même sens, au lieu de tester |z_t|(a² + b²) = 2 il est plus judicieux de tester z_t²a²+b²=4. On évite ainsi de recourir aux services inutilement long de la fonction racine carrée ; idem pour les fonctions circulaires et transcendantales (pourquoi pas fractales ?) chaque fois que l'on peut utiliser une table de constantes.

En général, l'optimisation dépend de la connaissance théorique du problème. Par exemple, si nous arrivons à démontrer qu'une fonction admet un axe de symétrie, les tests se réduisent à la moitié de son domaine de définition. Encore faut-il connaître ce domaine. N'oublions pas qu'au début des années 70, les fractales étaient encore des "monstres mathématiques", i.e. des processus au comportement excentriques par rapport aux mathématiques établies !

Aujourd'hui, l'EM est relativement si bien connu qu'il existe des algorithmes optimisés pour le produire "rapidement". L'un des pioniers dans le domaine de l'optimisation des fractales est Michael BARNSLEY avec son Iterative Function System (IFS). On doit aussi à Rico MARIANI, un brillant algorithme d'optimisation qui porte son nom !

1.3 - Courte inspection au coeur de la technologie des fractales... S'abstenir en cas de vertige mathinformatique

La finesse de l'image dépend du nombre maximum d'itération T et de la résolution graphique de l'ordinateur.

1.3.1. - La finesse de l'image

Le coût de la finesse est le temps à mettre pour la réaliser ; un arbitrage est alors nécessaire entre finesse et temps.

- Plus T est grand, plus les contours de l'EM sont précis. Théoriquement T+ est la condition nécessaire pour valider l'appartenance aux frontières de l'EM. Comme un programme non optimisé (voir ci-dessus) ne connaît pas les frontières, le T sera le même pour tous les points testés. Un transient d'ordre T est un point qui passe le test d'appartenance à l'EM jusqu'à la (T-1)ième itération pour finalement bifurquer vers l'infini à la Tième, d'où la nécessité d'un T très élevé pour valider l'appartenance.

- En pratique, l'utilisateur fixe T en tenant compte de la puissance de l'ordinateur (fréquence d'horloge, présence ou non d'un co-processeur numérique), et surtout de sa propre patience. A titre indicatif, certains experts estiment que sur un micro-ordinateur de 16 MHz sans co-processeur mathématique, avec une carte graphique de 1 Mo, T=512 produit un rendu visuel « correct » de l’EM.

1.3.2. Comme la Télé ...

- Il n'est pas nécessaire de garder allumé, l'écran qui n'est qu'un moniteur de la carte graphique, un peu comme l'enregistrement une émission de télé sans afficher les images à l'écran. Avec le multi-tâche (et les pseudo-multitâches) on peut même exécuter les programmes en processus parallèles ou en arrière plan (enregistrement d'une chaîne de télé pendant que l'on en regarde d'autres).

1.3.2 - Point logiques et Points physiques

Les points logiques sont des points au sens mathématique ; les points physiques sont des points de l'écran ou plus exactement de la carte graphique qui est dans l'unité centrale et non dans le moniteur. Sur une carte VGA 640x480 pixels (picture elements), il y a 307.200 points ou pixels à tester et à représenter.

Plusieurs modèles de correspondance co-existent avec le modèle canonique de magnification automatique : quelle que soit la zone du plan fournie par l'utilisateur, en coordonnées cartésienne représentées par un rectangle sur l'écran, la nouvelle image remplit tout l'écran.

1.3.3 - L'ensemble de Mandelbrot en entier

Si l'utilisateur veut voir l'EM en entier, soit le rectangle aux coins Nord-Ouest NO(-2, 1.2) et Sud-Est SE(1.2, -1.2), la correspondance (mapping) consiste à déterminer le pas (step) ou incrément sur l'axe des abscisses tel que l'étendue (range) de X soit égale à 640 : X_pas = [1.2 - (-2)] 640 = 0.005. De même pour l'axe des ordonnées Y_pas = [1.2 - ( -1.2)] 480 = 0.005. Les point logiques sont ainsi déterminés par incrémentation de 0.005 sur chaque axe à partir du coin Nord-Ouest vers le coin Sud-Est par une double boucle.

1.3.4 - La magnification automatique

Si l'utilisateur s'intéresse à la portion du plan aux coordonnées NO(-2, 0.9) et SE(-1.6, -0.9) les pas deviennent plus petit : X_pas = [-1.6 -(-2)] 640 = 0.000625. et Y_pas = [0.9 -(-0.9)] 480 = 0.00375, de telle sorte que le nombre de points logiques est toujours égal au nombre de pixels. En conséquence la petite zone du plan initial couvre maintenant tout l'écran comme un bout du texte recouvre la vue d'une loupe (magnifying glass) : c'est aussi simple que cela l’art de la magnification.

1.4 Terminologie des Mandelbroïdes

- Bassin attracteur fini cardioïde : le grand ensemble en forme de coeur ou de gingembre. L'autre attracteur est l'Infini. L’EM comporte un nombre infini de cardioïdes.

- Bourgeons ou Bébés ou Naines : les petits ensembles cardioïdes ayant un lien évident avec le grand bassin.

- Satellites : les petits ensembles n'ayant pas un lien évident avec le grand bassin. Il est suggéré qu'ils sont en fait reliés au noyau grâce par des filaments invisibles à cause du degré de magnification très élevé requis pour les voir.

Exemple de : (-1.78599 ; 0.045129) à (-1.72840,-0.03111)

- Filaments, la ligne pseudo-invisible (Cf. ci-dessus) entre la mère et l'enfant, une sorte de cordon ombilical...

- Lignes équipotentielles : les contours du bassin attracteur (Voir ci-dessous dans l'analyse spectrale).

- Mandelbroïde : Tout ensemble de la forme de l'EM dont l'information génératrice peut être légèrement différente. Par ex z_t+1 = (z_t)³ + c au lieu de "au carré" pour l'original EM.

- Transient d'ordre T (voir 1.3.1 c-avant)

Plaque N° 03: Vue "spectrale" de l'Ensemble de Mandelbrot

Section 2 - L'art de la magnification

Le propre des fractales mathématiques est de contenir une structure qui se reproduit infiniment en elle-même à des échelles de plus en plus petites ou de plus en plus grandes. Ces objets fractals sont scalants et invariants d'échelle : ils ont le même aspect quelque soit leur grossissement.

2.1 Exploration des coins et recoins fractals

Plaque N° 04 : Toujours le même ensemble, à l'infini !

(Self-similarity... objets scalants)

Plaque N° 05 : 1er Voyage aux confins de l'espace fractal :

Il n'y a pas de fin, l'infini est dans le fini !

Plaque N° 06 : Vue télescopique de L'Empire du Dragon...

Plaque N° 07 : Dragons ou Hippocampes (Sea-horses) ?

2.2 - A la recherche de satellites perdus ou inconnus

Plaque N° 08 : Ici Module MSN005 d'exploration des confins de l'univers de Mandelbrot - Apercevons Satellite Mx-1.8. A vous !

Plaque N° 09 : Arrivés à Mx-1.8. Encore de nouveaux Satellites surréalistes en vue. Approchons dangereusement "ligne de l'Univers" où se produit bifurcation vers l'Infini (risque de non retour). Retournons à la base EM. Stop et Fin.

Section 3 : La famille des Mandelbroïdes

3.1 Les ensembles de Julia

Les ensembles de Julia (EJ) sont construits avec une technique similaire à celle de l'ensemble de Mandelbrot. En fait, à chaque frontière de l'EM se dessine un EJ. MANDELBROT aurait découvert ou inventé son propre ensemble en expertisant les "monstres" mathématiques, dont les ensembles de Julia !

Plaque N° 10 : Une version très Mandelbroïde de

l'Ensemble de Julia

Plaque N° 11 Un ensemble de Julia dragonoïde !

3.2 D'autres Mandelbroïdes

PLAQUE N° 12 : Doublet Mandelbroïde - L'union de ces deux êtres a profondément transformé leur coeurs !

Plaque N° 13 : Appréciez ces Mandelbroïdes à la Newton

SECTION 4 : FRACTALES ET CHAOS

Les phénomènes chaotiques ont aussi un aspect fractal mis en évidence par le diagramme de bifurcation de Feigenbaum, l'attracteur étrange de Lorenz, le map de Martin, etc.

Plaque N° 14 : Images introductives aux fractales et au chaos

Extraites de MagSoftNews N° 2

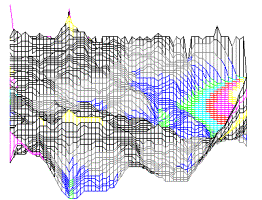
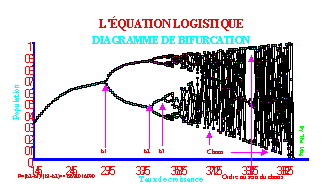Plaque N° 15 : Le Diagramme fractal de bifurcation de l'Equation Logistique : P_t+1=r*P_t(1-P_t)

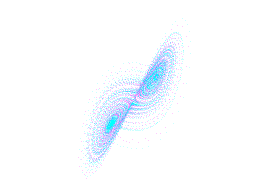
Plaque N° 16 : Le célèbre attracteur "étrange" de Lorenz : La trajectoire du système s'enroule à l'infini dans cet espace fini sans que jamais les points ne se croisent ... Étrange non ? La raison devient simple quand on se souvient que les fractales sont de dimension non entière. Or entre deux nombres, aussi proches soient-ils, il est toujours possible d'insérer un troisième nombre et ainsi de suite. On retrouve ainsi les Poussières de Cantor

Plaque N° 17 : Poussière de Cantor... Une fractale pour expliquer l'étrangeté des attracteurs fractals

SECTION 5 : D'AUTRES OBJETS FRACTALS

La puissance des fractales est réside dans leur aptitude à produire des objets complexes à partir d'une information extrêmement simple. Des codes génétiques appropriés et très concis, com-parables à l'ADN, permettent de reproduire les éléments de la nature : arbres, feuilles, montagnes, rivières, etc.

Plaque N° 18 : Paysage fractal. Pas évident pour tous !

Plaque N° 19 : Arbres fractals : on ne peut pas se tromper !

Plaque N° 20 : Organisme vivant .. une cellule bionique ?

Plaque 21 : Un coeur fractal émettant des ondes d'amour

CONCLUSION : A quoi servent les fractales ?

Pour le moment, les fractales sont appréciées du grand public pour la beauté des images produites. Pour la communauté scientifique les fractales sont liées aux systèmes dynamiques non linéaires, à la science naissante du chaos. Elles constituent la nouvelle géométrie ainsi qu'un des fondements du nouveau paradigme de la science. Etant donné qu'un code relativement simple produit des systèmes complexes, la recherche appliquée s'oriente vers la formalisation des codes générateurs à la base de la Nature, de l'Univers, de la de Vie, des Institutions.... Aujourd'hui, la plupart des codes sont implémentés dans un ordinateur en attendant peut-être un environnement ... plus naturel. MagSoftNews sera toujours au rendez-vous pour informer les Softivores des nouvelles avancées de la science dans cet univers fractal.

Supplément : L'affiche de FractalExpo 1993

By The Mag. University of Geneva, July 1993

1993 MagSoft - Citation avec indication de la source autorisée sans formalité - Réf. : MagSoftPub 2930701001

MagSoftNews

MSN n° 002 du 01/03/93 Revue des Softivores Editée par MagSoftPub

FRACTALES & CHAOS, Une Introduction

LES PRÉCURSEURS

Les fractales existent depuis la nuit des temps, mais elle n'ont connu de succès que récemment grâce à une théorie plus percutante : la théorie du chaos. Il y a longtemps, APOLLONIUS, JULIA FATOU, CANTOR, KOCK, SIERPINSKI nous ont offert une collection de monstres mathématiques. Mais pour propulser les fractales, il aura fallut que, contre EUCLIDE, Benoît MANDELBROT nous rappelle la nature fractale de notre univers : les nuages ne sont pas des sphères, les montagnes ne sont pas des cônes, les lignes des cotes ne sont pas des cercles, les écorces des arbres ne sont pas lisses, et l'éclair non plus, ne se déplace selon une ligne droite [The fractal geometry of nature].

IMAGES FRACTALES, le simple produit le complexe

Le propre des fractales est de contenir une structure souvent simple qui se reproduit infiniment en elle-même à des échelles différentes. Leur succès repose sur le fait qu'elles sont générées par des informations initiales simples qui, par une suite infinie d'itérations, reproduisent les éléments de la nature : arbres, feuilles, montagnes, rivières ou encore mieux, des images hautement esthétiques.

L'ÉQUATION LOGISTIQUE, Modèle de l'Écologie

Pour simuler l'évolution d'une population dans des conditions malthusiennes, les écologistes représentés par Robert MAY ont formulé et étudié la célèbre équation logistique : P_t+1=r*P_t(1-P_t) , où : P_t est la Population actuelle normée, soit en fait un taux d'occupation de l'environnement

P_{t+1 :} est la Population normée de l'instant suivant ; 1 : la nome, la population maximum possible dans les contraintes définies ; (1-P_t) est alors l'espace libre pour naître et vivre, le potentiel biotique ; (1-P_t) induit donc un feed-back dans le processus ; r est le paramètre de contrôle ou taux de croissance ou de fécondité etc. L'équilibre à long terme de ce beau petit monde (ou modèle mathématique) dépend de P_{0 :} la population initiale et du paramètre de contrôle r.

LA ROUTE DE DOUBLEMENT DE PÉRIODE VERS LE CHAOS

En étudiant les valeurs d'équilibre des systèmes dynamiques comme l'équation logistique, on constate que :

- Tant que (r<b1) un léger accroissement de r entraîne une hausse de la valeur d'équilibre de la population. C'est ce qui était généralement admis.

- La première bifurcation a lieu à r=b1. Quand (b1<r<b2), la valeur d'équilibre oscille entre deux valeurs pour prendre alternativement l'une et l'autre. Quand (b2<r<b3), quatre valeurs d'équilibre sont alors possibles. René THOM a exprimé les bifurcations en termes de Théorie des catastrophes.

- Au-delà de r=b3, le système peut prendre un grand nombre de valeurs d'équilibre exhibant brusquement un comportement apparemment imprévisible, chaotique. Cette cascade de bifurcations est dénommée "la route vers le chaos".

En fait, le nombre de valeurs d'équilibre entre la (i)ème et la (i+1)ème bifurcation n’est rien d’autre que 2⁽ⁱ⁺¹⁾. Entre seulement la 8^ième et la 9^ième bifurcation, il y a 2⁹ soit deux milliards d’équilibres qui s’alternent, créant l’illusion du désordre, le chaos !

L'ORDRE ÉMERGE DU CHAOS

La théorie du chaos n'est pas comme son nom peut laisser croire une théorie de désordre, ni une théorie pessimiste. Au contraire, elle montre que dans la zone où le phénomène a un comportement chaotique, en regardant de près, en mettant la loupe ou le microscope on y retrouve le même motif [pattern] exhibé par le processus. La zone chaotique est fractale. Dans ce désordre apparaît un ordre absolu, la répétition infinie de la même fractale. Sur le graphique apparaît grâce à la magnification une fenêtre dans le chaos semblable à celle séparant les deux branches après b1 . Selon Ilya PRIGOGINE, le chaos et les processus dissipatifs loin de l'équilibre seraient indispensables à la vie.

UN DÉSORDRE A UN RYTHME ORDONNÉ

Un chaos réellement aléatoire serait sans utilité pour la Science et les prévisions. Edward LORENZ, le pionnier, était météorologue. Heureusement, Mitchell FEIGENBAUM a découvert que le désordre se produit à un taux ordonné qui est devenu sa constante F (voir sur le diagramme de bifurcation). Ainsi on peut prévoir le "moment" exact ou plutôt la valeur critique du paramètre de contrôle où a lieu chaque bifurcation, car les systèmes paraboliques non-linéaires bifurcatifs obéissent à la constante de Feigenbaum F = 4,6692016090... Comme quoi, l'univers recèle bien des chiffres transcendants, les clés de la géométrie, comme p (rapport constant entre la circonférence et le diamètre de tout cercle) et e (le nombre d'Euler, le même qui est immortalisé sur le billet de 10 Francs suisses) dont la découverte permet aux êtres humains de lui arracher de plus en plus de ses secrets...

VERS UNE NOUVELLE SCIENCE ou un nouveau paradigme de la science

Les fractales et la théorie du Chaos, en élargissant le champ de la géométrie vers davantage de réalité ont suscité beaucoup d'espoir (et quelques succès déjà) dans tous les domaines dont la météorologie, l'écologie, la biologie, la cardiologie, la biochimie, la physique, l'astronomie, l'économie, etc. Partout, les chercheurs tentent de retrouver les processus fractals-chaotiques qui seraient à la base de l'Univers, de la de Vie, de la dynamique des Institutions, des cours sur les marchés financiers.

L'ENJEU FRACTAL

Si on sait que la connaissance de telles lois pourrait permettre de fonder un nouveau paradigme de La Science en même temps que faire gagner, ceteris paribus, de sommes faramineuses aux premiers ou aux meilleurs, on comprend pourquoi cette science numérique alliant les mathématiques (outil universel de modélisation), et l'informatique (outil permettant de simuler in electro en quelques secondes, ce que Dame Nature mettrait des années ou des millénaires à accomplir), ne laisse indifférents ni les savants soucieux d'aider le monde, ou en quête de gloire (en témoigne la bataille chaotique des fondateurs entre eux pour se faire reconnaître et/ou pour tenter de diminuer la valeur des recherches leurs concurrents), encore moins les jokers de la finance nouvelle...

By The Mag. University of Geneva, March 1993

1993 MagSoft - Citation avec indication de la source autorisée sans formalité - Réf. : MagSoftPub 2930301001